3.2.4 Factor

Integers can be expressed as the product of factors: 6=2⋅3 Similarly, polynomials can be expressed as the product of simpler polynomials: x^2+4⋅x+3=(x+1)⋅(x+3) and matrices can be expressed as the product of simpler matrices:

[(1, 2), (3, 4)]=[(1, 0), (1/3, 1)]∘[(3, 4), (0, 2/3)].

Factoring decomposes an expression into a product of other expressions. The process ends when the other expressions cannot be factored further. For integers, decomposition into factors ultimately results in the product of primes. For polynomials, decomposition ends when each factor is an irreducible polynomial. And for matrices, LU-decomposition is performed.

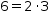
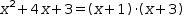
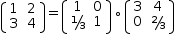
There are several ways to perform factoring in Myron. Polynomials can be factored symbolically by Polynomials Factor (not to be confused with the factoring described in this section) and numerically by Expressions Newton . Both make use of Polynomial Division . This page starts with the simplest way, using Factor on the fast-action bar.

Factor performs different operations depending on whether the subject is primary, unary or binary.

If the subject is an integer, factor will attempt to find the integer factors of the subject and will result in a product of integers representing those factors. For example, factoring 12345678905 results in 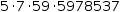5⋅7⋅59⋅5978537. If the result is the same as the subject, it means one of two things: either the subject was prime or the factoring ran out of time. You can tell the latter from the response time of the result.

If the subject is a unary negation, factoring produces the product of -1 with the absolute value of the subject. That is, 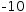-10 factors to -1⋅10.

If the subject is a binary operator, factor uses the rightmost operand to supply a candidate. If the candidate can be factored from the left operand, it is used. Otherwise, the candidate is refined by examining its own operands.

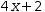
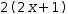
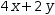
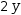
For example, in 4⋅x+2 the candidate is 2 and the expression factors to 2⋅(2⋅x+1). But in 4⋅x+2⋅y the candidate is 2⋅y. Since the candidate is not a factor of the left subexpression, its own subexpressions are examined, with y and 2 being considered in turn. y is not a factor of the left expression, but 2 is. The final result is 2⋅(2⋅x+y)

If the subject is a matrix, Factor performs LU-decomposition to produce a lower-diagonal and upper-diagonal matrix whose matrix product is the same as the original.

Try factoring the following expressions. Also try using Simplify and other manipulations to get back the original expression.

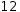
12 (then try to recombine the factors so you have 4*3)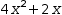
4⋅x^2+2⋅x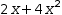
2⋅x+4⋅x^2
3⋅y^2+12⋅y (hint, factor 12 first)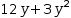
12⋅y+3⋅y^2
x^2+4⋅x+3 (see §3.4.7 Polynomial Division)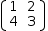
[(1, 2), (4, 3)]
[(10, 10, 71), (5, 1, 3), (, -15, 1, 6)]